09_WeightedRandomMelody.zip
Download

Description

Up to this point, we have been using the metro object to provide the pulse for our generative music. Heretofore, we will use the tempo object which allows us to express the tempo in beats per minute rather than milliseconds. What is more, the optional second and third arguments to tempo allow us to express a default duration as a fraction. In the patcher above, the tempo is set to 1/4-note equals 120 beats per minute. Notice how this has opened up a whole new world of durations to us. Not just 1/4 note, 1/8 note, 1/16 note, 1/32 note, but also 1/1 (whole note), 1/2 (half note), 1/3 (note), 1/5 note, etc. We can now easily represent any duration 1/n, where n is a positive integer. Something the experimental American Henry Cowell could only dream of in his book New Musical Resources (1930).

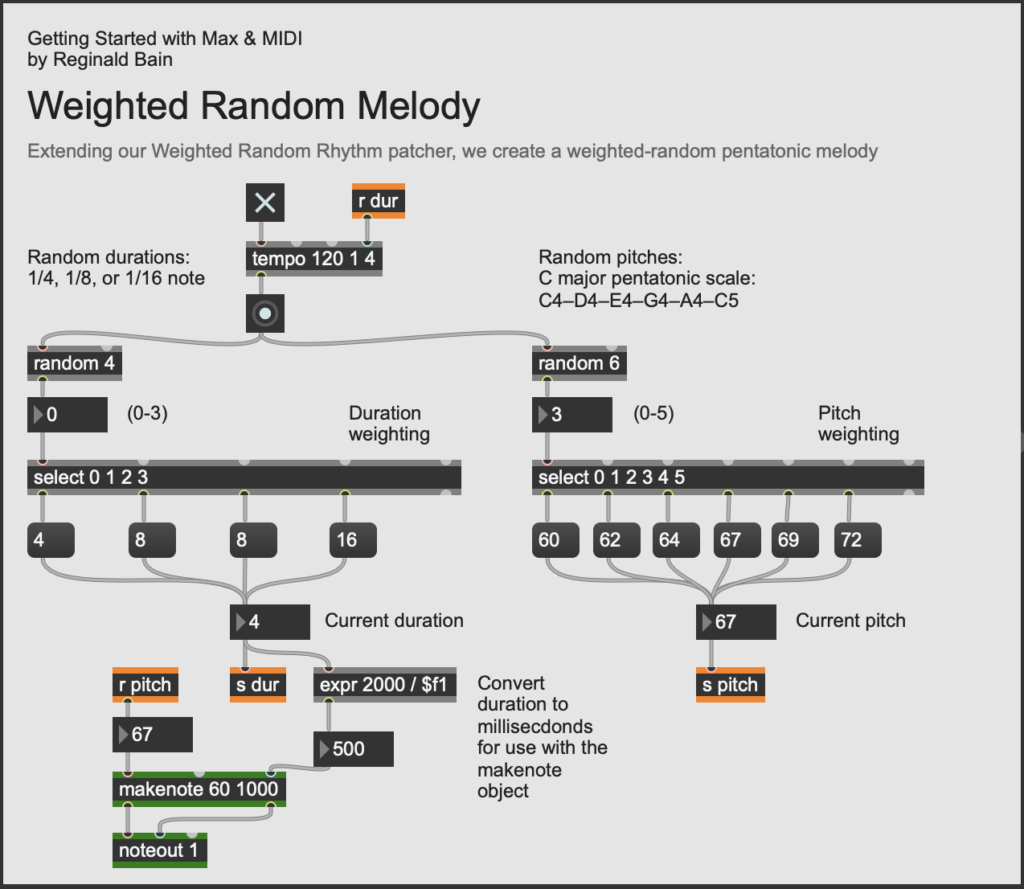
Let's create a random melody. For pitch content, let's simply select our notes from a major pentatonic scale on C4: 60, 62, 64, 67, 69, 72. Extending our Weighted Random Rhythm patchern (07c Weighted Random Rhythm), we create a weighted-random pentatonic melody. The patcher is split into two sections. The left side determines the duration. The right side determines the pitch. The left side is essentially the same code block as 07c Weighted Random Rhythm, except we express durations as fractional values to control the tempo object. Notice how the current duration (4, 8, 8, 16) is fed into the second argument of the tempo object via a send-receive pair. What is more, the makenote object requires q duration in milliseconds. This calculation is easy to make. At 120 bpm, a whole note (1/1) is 2000 ms., so we must simply divide the possible durations 4, 8, and 16 into 2000 ms. using and expr object.

Exploration

As the patcher currently stands, there are 6 equally weighted pitches. Try weighting one of the pitches to make the melody more interesting. Of course, you can also add more pitch messages and corresponding arguments to the select object to expand the number of pitches from which you are selecting. You could even change the scale entirely to enter a new harmonic realm.

Objects

Further Reading